이번 게시물은 재귀(순환)함수에 대해 글을 작성하려 한다.
재귀의 정의는 다음과 같다.
컴퓨터 과학에 있어서 재귀(再歸, Recursion)는 자신을 정의할 때 자기 자신을 재참조하는 방법을 뜻하며, 이를 프로그래밍에 적용한 재귀 호출(Recursive call)의 형태로 많이 사용된다.
재귀함수는 여러가지 경우에서 많이 사용되는데, 대표적으로 계승(factorial)을 구하는 데 사용된다.
계승을 구하는 코드는 다음과 같다.
|
1
2
3
4
5
6
7
8
9
|
unsigned int factorial(unsigned int n)
{
if (n <= 1)
return 1;
else
return n * factorial(n-1);
}
|
cs |
위의 코드를 보면 함수 내에서 자기 자신(함수)를 호출하는 것을 볼 수 있다.
저런식으로 함수 내에서 자기 자신(함수)를 다시 호출하는 것을 재귀라고 한다.
여러가지 경우에서 재귀를 많이 사용하지만, 이번 게시물에서는 완전탐색에서 재귀를 사용하는 방법을 작성하려 한다.
1. 완전 탐색(Brute-Force Search)
Brute-Force라는 이름이 생소하기도 하고, 완전 탐색이라고 단어만 딱 들으면 되게 어려워보이는데, 사실 별거 없다.
나올 수 있는 모든 경우의 수를 다 확인하는 탐색 방법을 완전 탐색이라 한다.
예를 들어서 3명이서 가위바위보 게임을 한다고 생각해보자.
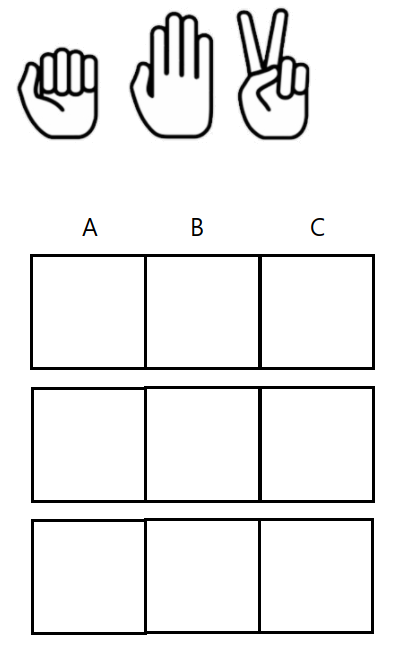
가위바위보 게임에서 A, B, C 는 가위, 바위, 보 중에 하나를 낼 것이고 한 번의 게임을 했을 때 결과는 아래처럼 다양하게 나올 것이다.

다른 예시로 1, 2, 3 3장의 카드중에 한 장씩 총 3장을 뽑는다고 생각해보자. 단, 같은 카드를 중복으로 뽑을 수 있다.
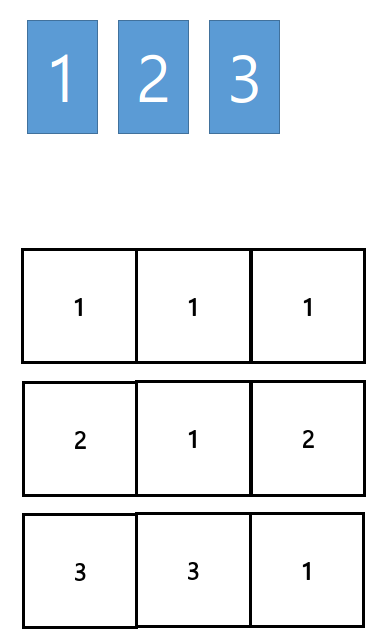
마찬가지로 여러가지 경우의 수가 나올 것이다.
이를 코드로 옮기면 어떻게 작성할 수 있을까?
1-1. 1장의 카드
조금 더 쉽게 생각해서 먼저 1, 2, 3, 총 3장의 카드 중에 1장을 뽑는 경우의 수를 생각해보자.
경우의 수는 아래와 같을 것이다.

코드로 나타낸다면 단순하게 반복문 1번으로 모든 경우의 수를 구할 수 있다.
|
1
2
3
4
5
6
|
for(int i = 1; i <= 3; i++){
//결과 값
cout << i << " ";
}
|
cs |
1-2. 2장의 카드
그 다음으로 1, 2, 3, 총 3장의 카드 중에 2장을 뽑는 경우의 수를 생각해보자.

위의 1-1. 1장의 카드 에서 반복문을 하나 더 중첩시켜 2중 반복문으로 아래와 같이 구현할 수 있다.
|
1
2
3
4
5
6
7
8
|
for(int i = 1; i <= 3; i++){
for(int j = 1; j <= 3; j++){
//결과 값
cout << i << " " << j << " ";
}
}
|
cs |
1-3. 3장의 카드
그렇다면 1, 2, 3, 총 3장의 카드중에 3장을 뽑는 경우의 수는?
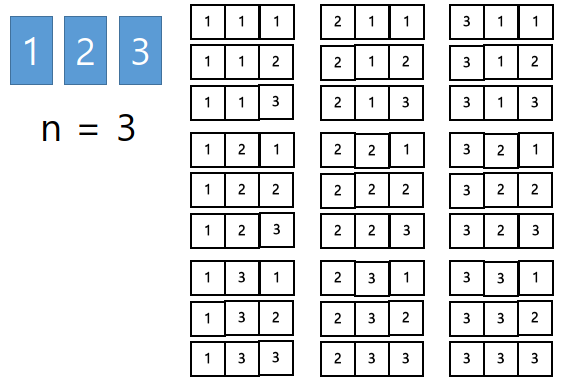
눈치 챘겠지만, 고를 카드의 수가 많아질 수록 반복문이 중첩된다.
|
1
2
3
4
5
6
7
8
9
10
|
for(int i = 1; i <= 3; i++){
for(int j = 1; j <= 3; j++){
for(int k = 1; k <=3; k++){
//결과 값
cout << i << " " << j << " " << k << " ";
}
}
}
|
cs |
고를 카드의 수가 적다면 반복문을 중첩시켜서 어떻게든 모든 경우의 수를 계산해보겠지만, 아래처럼 10장의 카드를 골라야 한다면 코드가 상당히 복잡해질 것이다.

이를 해결해줄 방법이 재귀(순환)함수 이다.
2. 재귀함수
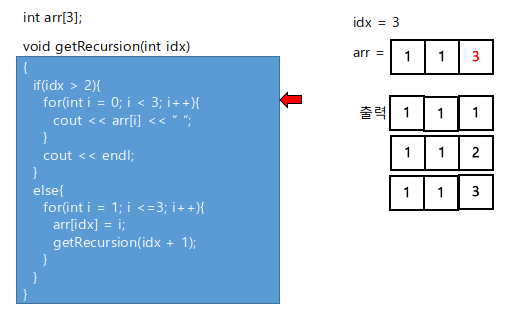
완전탐색을 위한 재귀함수는 사용자에 따라 다르지만, 내가 자주 사용하는 틀은 아래와 같다.

위의 코드는 1, 2, 3, 총 3장의 카드중에 임의로 3장을 고르기 위한 코드이다.
int arr[3]은 고를 카드의 수(출력할 숫자의 갯수)에 맞춰 배열을 생성한 것이다.
위의 그림에 써있는 것처럼 if문 안의 for문에서의 숫자 3은 출력할 숫자의 갯수,
else문 안의 for문에서의 숫자 3은 출력할 숫자의 숫자 범위, 즉, 카드의 번호 1, 2, 3 을 의미한다.
void getRecursion(int idx) 에서 idx는 현재 몇번째 카드를 고르고 있는지 판단하기 위한 숫자이다.
메인함수에서 재귀함수를 다음과 같이 호출하는데,

idx를 0으로 시작해서 +1씩 더해가면서, 0번 index, 1번 index, 2번 index에 순서대로 저장한다.
메인함수에서 getRecursion(0)을 호출하면, 재귀함수는 아래와 같이 동작할 것이다.

먼저 idx가 0인 상태로 함수안에 들어오고 idx = 0 이므로, if문이 아닌 else문으로 들어가게 된다.

arr의 idx( = 0 ) 번째 index에 1( 카드의 범위 1~3 중 첫 번째 )이 들어가게 된다.

배열의 0번째에 1을 넣은 후 idx( = 0 ) 에 1을 더한 값을 매개변수로 다시 재귀함수를 호출한다.

그러면 idx가 1인 상태로 새로운 getRecursion함수가 동작하게 되고

idx 값이 1 이므로 2보다 크지 않은 값이니까, else문으로 다시 들어가게 된다.

arr의 idx( = 1 ) 번째에 1( 카드의 범위 1~3 중 첫 번째 )이 들어가게 된다.

배열의 1번째에 1을 넣은 후 idx( = 1 ) 에 1을 더한 값을 매개변수로 다시 재귀함수를 호출한다.

idx는 2인 상태로 새로운 getRecursion함수가 동작하게 되고

idx 값이 2 이므로 2보다 크지 않은 값이니까, else문으로 다시 들어가게 된다.

arr의 idx( = 2 ) 번째에 1( 카드의 범위 1~3 중 첫 번째 )이 들어가게 되고,

배열의 2번째에 1을 넣은 후 idx( = 2 ) 에 1을 더한 값을 매개변수로 다시 재귀함수를 호출한다.

idx는 3인 상태로 새로운 getRecursion함수가 동작하게 되고

idx 값이 3 이므로 2보다 큰 값이니까, if문으로 들어가게 된다.

if문에서는 arr에 저장되있는 값을 출력한 후,

idx = 3인 재귀함수가 종료되므로, idx = 2 에서 재귀함수를 호출한 시점으로 다시 돌아간다.
else문 안의 반복문에서 i값이 +1 되어서 arr의 idx( = 2)번째에 i값( = 2)이 들어가게 된다.
그 후에 다시 getRecursion(idx + 1)을 호출해서

idx = 3인 상태로 getRecursion이 동작한다.
idx = 3 이므로 2보다 크니까 if문으로 들어가게 되고

다시 arr에 저장된 값들을 출력한다.
if문에서 출력을 마친후 idx = 3인 getRecursion이 종료되고,

다시 idx = 2에서 getRecurion을 호출한 후의 시점으로 이동한다.
else문 안의 반복문에서 i는 +1되서 3이되고, arr의 idx( = 2 )번째 i( = 3 )을 넣어준다.
그 후에 다시 getRecursion(idx + 1)을 호출한다.

idx = 3 이므로 2보다 크니까 if문으로 들어가게 되고
다시 arr에 저장된 값들을 출력한다.
if문에서 출력을 마친후 idx = 3인 getRecursion이 종료되고,
다시 idx = 2에서 getRecurion을 호출한 후의 시점으로 이동한다.
idx = 2에서 else문 안의 반복문이 1에서 3까지 전부다 돌았으므로, idx = 2인 getRecursion 또한 종료된다.

idx = 1인 getRecursion에서 getRecursion(idx+1)을 호출한 후의 시점으로 돌아오고,

idx = 1인 상태에서의 for문이 동작해서 i = 2가 되고,
arr의 idx( = 1 )번에 i( = 2 )를 넣어준다.

그 후에 getRecursion(idx+1)을 다시 호출한다.

idx = 2 인 상태에서 새로운 getRecursion이 동작하게 되고,

idx( = 2 )는 2보다 크지 않으므로 else문으로 들어간다.

arr의 idx( = 2 )번째에 i( = 1 )을 넣어주고,

getRecursion( idx + 1 )을 호출한다.

idx가 3인 새로운 getRecursion이 만들어지고,
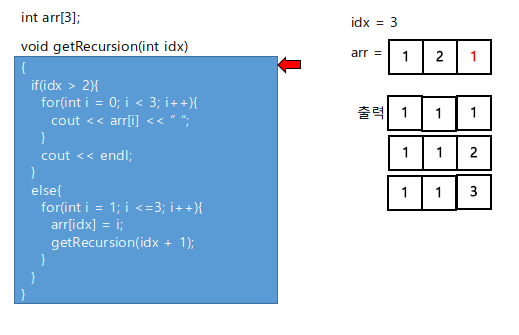
idx( = 3 )이 2보다 크므로 if문 안으로 들어가게 된다.

if문에서 저장되있는 arr값들을 다시 출력하게 된다.

위의 같은 과정을 계속 반복하면 아래와 같이 호출이 계속 되고,


최종적으로 아래와 같은 결과값을 얻을 수 있다.

사실 재귀함수는 숫자가 커지면 연산양이 많아지기도 하고, 탈출 조건을 걸어주지 않는다면 무한루프에 빠질 수도 있어서 개인적으로 별로 좋아하진 않는다.
하지만 재귀함수를 꼭 사용해야할 경우들이 몇가지 있어서 코딩테스트 준비를 위해 필수로 알아야한다.
이해가 되지 않는다면 천천히 글을 다시 읽어보거나, 다른 분의 블로그를 참고하면서 꼭 재귀에 대해 이해하고 넘어갔으면 한다.
'Legacy' 카테고리의 다른 글
| [C++#4-1] DFS (0) | 2021.06.13 |
|---|---|
| [C++#4] 탐색 (0) | 2021.06.10 |
| [C++#2-4] 확산 알고리즘 (0) | 2021.06.08 |
| [C++#2-3] 밀기 알고리즘 (0) | 2021.06.08 |
| [C++#2-2] 이동 알고리즘 (1) | 2021.05.30 |